Markov Chain Monte Carlo (MCMC) methods represent a powerful intersection of two fundamental concepts in probability and statistics: Markov chains and Monte Carlo techniques. These methods have revolutionized our ability to solve complex problems in various scientific fields, from physics to biology, and from economics to machine learning.

The foundation of MCMC lies in the concept of Markov chains, introduced by Russian mathematician Andrey Markov in the early 20th century. Markov chains are mathematical systems that transition from one state to another in a sequential process. The key characteristic of a Markov chain is its “memoryless” property: the probability of transitioning to a future state depends only on the current state, not on the sequence of events that preceded it. This property makes Markov chains particularly useful for modeling complex systems in fields ranging from physics to economics, where the future state of a system can be predicted based solely on its present state.

The Monte Carlo component of MCMC has its roots in the 1940s, during the Manhattan Project at Los Alamos. Scientists like Stanislaw Ulam and John von Neumann developed these methods to solve complex problems related to nuclear physics. The name “Monte Carlo” was coined as a nod to the famous casino, reflecting the inherent randomness of the approach. Monte Carlo methods use repeated random sampling to obtain numerical results, particularly for systems too complex for analytical solutions.

The intent of this post is to provide an introduction to Monte Carlo Markov Chain (MCMC) methods. In no way is this an attempt to replace a textbook, or get into graduate level topics. Rather, it is aimed to provide background and a working understanding for anyone with a moderate background in Bayesian Statistics, math, and python. Our end goal for this post is to understand the Metropolis-Hasting Algorithm, one of the most famous MCMC methods.

It’s layout is as follows

• Introduction to Markov Chains
• Summary of MCMC Methods
• Learning the Metropolis-Hasting Algorithm

When appropriate, I’ve provided the code to show how particular ideas can be implemented. To see the full code, including what I used for visualizations, check out the colab notebook at https://github.com/HarrisonSantiago/WebsiteNotebooks

If you notice an error or can think of a good addition, please feel free to contact me at contactme@harrisonsantiago.com

Introduction to Markov Chains

Before we dive into the specifics of Markov chains, let’s consider what they are and why they’re important. In many real-world situations, we encounter systems that change over time in a probabilistic manner. For example, think about the weather: tomorrow’s weather is likely influenced by today’s weather, but not necessarily by what happened a week ago. Markov chains provide a stochastic framework for modeling such systems.

For a more formal definition, a discrete-time Markov chain is a sequence of random variables \( X_{0},X_{1},X_{2},…\) with the Markov property, namely that the probability of moving to the next state depends only on the present state and not on the previous states. This can be formalized as:

\[ \Pr(X_{n+1}=x\mid X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{n}=x_{n})=\Pr(X_{n+1}=x\mid X_{n}=x_{n}), \]

The possible values of \(X_i\) form a countable set \(S\) called the state space of the chain. You can think of the state space as all of the possible situations our system can be in. Building off this, a trajectory describes the actual path the system takes through this state space over time (i.e. \(X_0 = A, X_1 = A, X_2 = C, \ldots\)). As the Markov chain evolves, it creates a trajectory by moving from one state to another according to the transition probabilities. By analyzing these trajectories, we can gain insights into the long-term behavior of the system, including which states are visited most frequently and whether the system tends to settle into particular patterns or cycles.

Example

In practice, Markov Chains are often visualized in the form of directed graphs. Here each node represents a state \(X_i\), and the edge \((X_i, X_j)\) represents \(\Pr(X_{n+1} = j \mid X_n = i)\).

Here we have a visualization of a Markov Chain with three states (A, B, and C).

Frequently, the changes in the state of the system are called transitions, and the probabilities associated with these changes are known as transition probabilities. A particular process can be defined by a transition matrix describing the probabilities of transitions. Following standard convention, in a transition matrix \(T\), element \(T_{i,j}\) is the probability of going from state \(i\) to state \(j\).

For our example above, our Transition Matrix is simply

\[ \begin{bmatrix} 0.5 & 0.3 & 0.2 \\ 0.2 & 0.15 & 0.65 \\ 0.6 & 0.1 & 0.3 \end{bmatrix} \]

Where \(T_{ij}\) is the probability of going from state \(i\) to state \(j\). To create a trajectory of length \(n\), you would first select an initial state \(X_0\). Then, for each step \(k\) from 1 to \(n\), you would choose the next state \(X_k\) based on the probabilities given in the row of the transition matrix corresponding to the current state \(X_{k-1}\). This process is repeated \(n\) times to generate the complete trajectory \((X_0, X_1, …, X_n)\).

Below we have the basic code needed to make a Markov Chain for the directed graph above, and how to create a trajectory.

import numpy as np

class MarkovChain:
    def __init__(self, transition_matrix, states):
        self.transition_matrix = np.array(transition_matrix)
        self.states = states
        self.state_index = {state: idx for idx, state in enumerate(states)}
        self.current_state = None

    def set_initial_state(self, state):
        if state not in self.states:
            raise ValueError("State not in the list of possible states.")
        self.current_state = state

    def next_state(self):
        if self.current_state is None:
            raise ValueError("Initial state not set.")

        current_index = self.state_index[self.current_state]
        next_state_index = np.random.choice(len(self.states), p=self.transition_matrix[current_index])
        self.current_state = self.states[next_state_index]
        return self.current_state

    def generate_states(self, num_steps):
        if self.current_state is None:
            raise ValueError("Initial state not set.")

        states = [self.current_state]
        for _ in range(num_steps):
            states.append(self.next_state())
        return states
    

If we create a model for the example shown above, we can easily generate a trajectory that is 10 steps long. Here is an example of how to do that, and a visual for the resulting trajectory.

# Define the transition matrix
transition_matrix = [
    [0.5, 0.3, 0.2],
    [0.2, 0.15, 0.65],
    [0.6, 0.1, 0.3]
]

# Define the states
states = ["A", "B", "C"]

# Create the Markov Chain
mc = MarkovChain(transition_matrix, states)

# Set the initial state
mc.set_initial_state("A")

# Generate the next 10 states
generated_states = mc.generate_states(10)
print("Generated states:", generated_states)

mc.plot_transitions(generated_states)
    

Now let’s look at how often a transition \(X_i \rightarrow X_j\) happens. If we sum up the number of times each transition happens and then normalize, ideally we would recover the probabilities that we defined in \(T\). Below, we will show the normalized frequency of each transition, and then the probabilities in the same style of \(T\).

Unsurprisingly, we start to recover our original transition matrix. In fact, we can show how our approximation improves as we go on longer and longer trajectories. To do this we will go on trajectories of increasing size, and compute an approximation \(T’\) at the end of each. The plot on the left shows the Euclidean distance between the \(T\) and \(T’\) for each trajectory, and the right shows \(T’\).

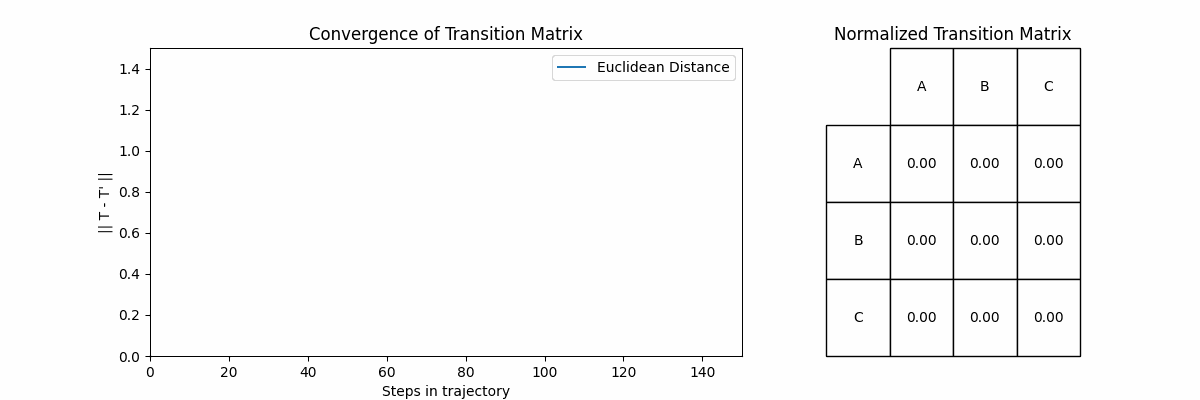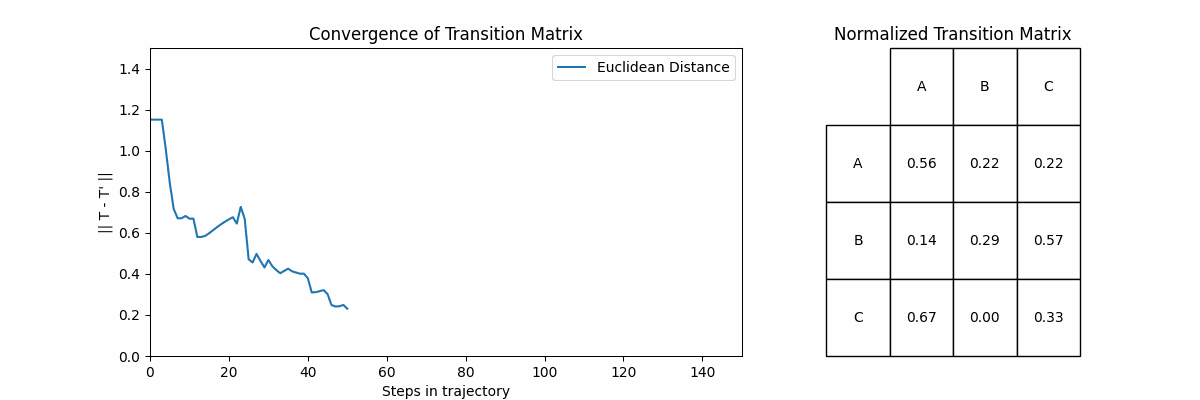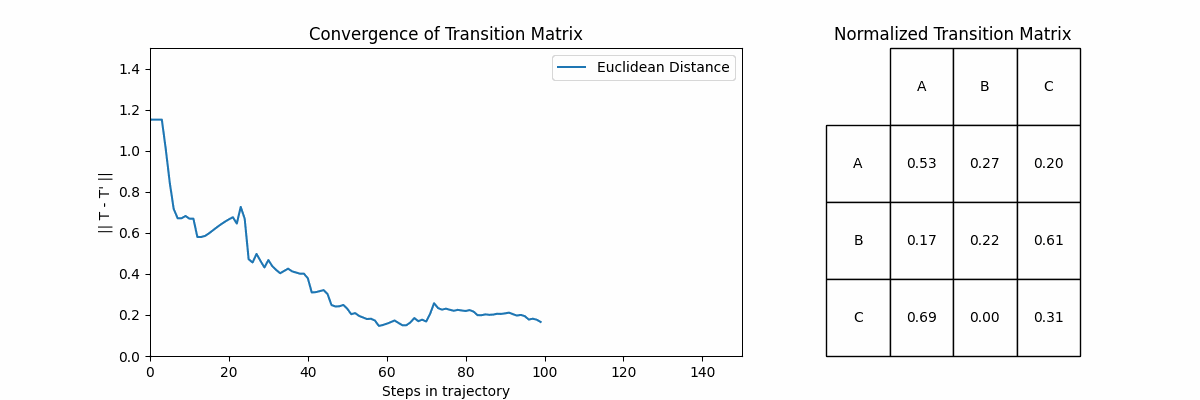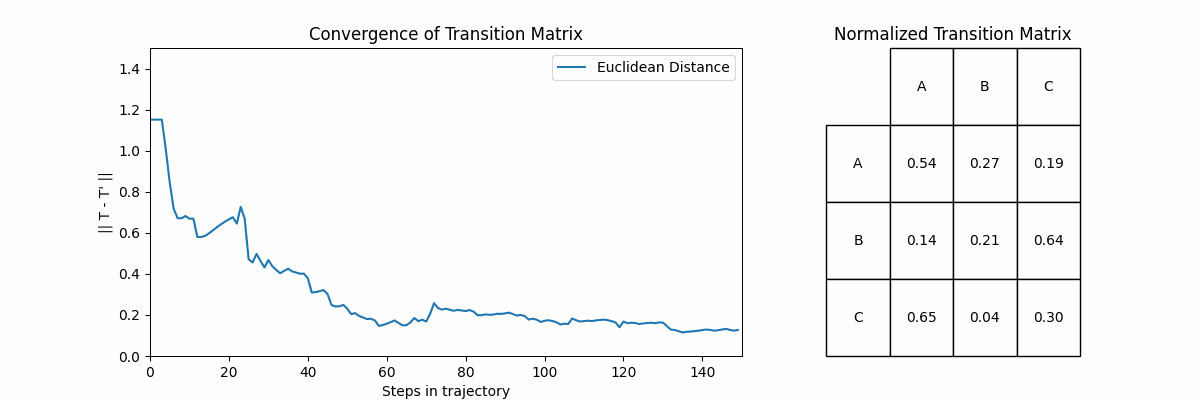
Let’s explore two fundamental concepts in Markov Chains: accessibility and communication between states.

Accessibility: We say a state \(j\) is accessible from state \(i\) (denoted as \(i \rightarrow j\)) if there’s a non-zero probability that the system, starting in state \(i\), will eventually transition to state \(j\). It’s crucial to understand that this transition doesn’t need to occur in a single step. For example, even if the direct transition probability \(\Pr(X_1 = A \mid X_0 = B) = 0\), state \(A\) could still be accessible from \(B\) if there exists an intermediate state \(C\) such that \(\Pr(X_1 = C \mid X_0 = B) \neq 0\) and \(\Pr(X_2 = A \mid X_1 = C) \neq 0\).

Communication: States \(i\) and \(j\) are said to communicate (denoted as \(i \leftrightarrow j\)) if they are mutually accessible, i.e., if both \(i \rightarrow j\) and \(j \rightarrow i\). A communicating class is defined as the largest set of states where every pair of states within the set communicates with each other.

Building on these concepts, we can define an important property of Markov chains. A Markov chain is considered irreducible if its entire state space forms a single communicating class. In other words, an irreducible Markov chain allows for the possibility of transitioning from any state to any other state, given enough time.

As we explore Markov chains further, we encounter a fundamental concept: the stationary distribution. This distribution, denoted by \(\pi\), is a vector that satisfies the equation \(\pi T = \pi\), where \(T\) is the transition matrix. The stationary distribution has a profound interpretation: in the long run, regardless of the initial state, the proportion of time the chain spends in state \(c\) approaches \(\pi_c\).

The concepts of accessibility, communication, and irreducibility play crucial roles in understanding stationary distributions. In irreducible chains, where all states communicate (i.e., every state is accessible from every other state), a unique stationary distribution is guaranteed to exist for finite-state systems. This distribution assigns positive probabilities to all states, reflecting the chain’s long-term behavior.

For a Markov chain to converge to its stationary distribution, it needs to be “non-pathological”. This requirement encompasses two key properties:

• Aperiodicity: The chain doesn’t cycle through a subset of states in a fixed pattern. This is related to the concept of accessibility, as it ensures that the chain can return to any state at irregular intervals.
• Connectedness: This property is equivalent to irreducibility. It means that for any two states, there exists a path with non-zero probability connecting them. In other words, the entire state space forms a single communicating class.

When a Markov chain is both irreducible (connected) and aperiodic, it is called ergodic. Ergodic chains not only possess a unique stationary distribution but also converge to this distribution over time, irrespective of the initial state. This convergence property is what allows us to “recover” both the transition matrix \(T\) and the stationary distribution \(\pi\) as the number of steps \(n\) increases in a sufficiently long random walk.

It’s important to note that in non-irreducible chains, multiple stationary distributions may exist, each corresponding to a closed communicating class. The concept of accessibility helps determine which states have positive probability in these distributions: if state j is inaccessible from state i, and i has positive probability in a stationary distribution, then j must have zero probability in that distribution.

Those of you who have taken a linear algebra course may recognize \(\pi\) as the left eigenvector of \(T\). As such, we can find it analytically.

Take the transpose of \( T \):

\[ T^\top \]

2. Find the eigenvectors and eigenvalues of \( T^\top \):

\[ T^\top v = \lambda v \]

where \( \lambda \) represents the eigenvalues and \( v \) represents the eigenvectors of \( T^\top \).

3. Identify the eigenvector corresponding to the eigenvalue 1:

\[ T^\top v = 1 \cdot v \]

4. Normalize the left eigenvector to sum to 1:

\[ \pi = \frac{v}{\sum v} \]

where \( \pi \) is the normalized left eigenvector of \( T \).

Which can be accomplished by the following code. If we run it for our example transition matrix we get.

def find_stationary_distribution(transition_matrix):
      # Find the eigenvalues and eigenvectors
      eigenvalues, eigenvectors = np.linalg.eig(transition_matrix.T)

      # Find the eigenvector corresponding to the eigenvalue 1
      stationary_vector = eigenvectors[:, np.isclose(eigenvalues, 1)]

      # Normalize the eigenvector to sum to 1
      stationary_distribution = stationary_vector / stationary_vector.sum()

      return stationary_distribution.real.flatten()

>>> [0.47111111 0.20444444 0.32444444]
    

However, if we don’t know the transition matrix, we easily estimate it by going on a long walk and looking at the percentage of time we are in each state. Let’s look at how our estimate develops as we go only longer and longer trajectories.

An interesting use case is that we can use these estimations to recover the unknown transition and stationary matrices of any Markov model. This is a significant point, as the ability to recover the stationary distribution of a Markov chain is crucial for understanding the long-term behavior of the system it models. A stationary distribution, when it exists, represents the equilibrium state of the Markov chain – the probability distribution that the chain converges to as it evolves over time, regardless of the initial state. In other words, the stationary distribution of a Markov chain provides a probability distribution over all possible states of the system, allowing you to construct arbitrary sampling distributions. This is the driving force behind MCMC methods.

Introduction to Markov Chain Monte Carlo (MCMC) Methods

Monte Carlo Methods

Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to solve numerical problems that may be deterministic in nature. These methods are used to approximate mathematical systems, performing tasks like integration, optimization, and simulation by generating a large number of random samples from a probability distribution. By averaging the results of these samples, Monte Carlo methods provide estimates that converge to the true values as the number of samples increases.

What makes Monte Carlo methods particularly valuable is their ability to tackle deterministic problems using probabilistic approaches. This counterintuitive technique often proves more efficient than traditional deterministic methods, especially for high-dimensional problems or systems with many interacting parts. For example, in physics, calculating the properties of a complex molecule with many atoms can be computationally infeasible using exact methods, but Monte Carlo simulations can provide accurate approximations in a fraction of the time.

Broadly speaking, there are four steps to any Monte Carlo method:

1. Define a domain of possible inputs
2. Generate inputs randomly from a probability distribution over the domain
3. Perform a deterministic computation of the outputs
4. Aggregate the results

As as example, let’s create a Monte Carlo Method for estimate the value of pi. To do this, our four steps are:

1. We’ll constrain a circle to fall in between -1 and 1
2. Generate sample from the uniform distribution on that domain.
3. We’ll determine if a point is inside the radius or outside.
4. To aggregate the results we will say \(\left(\frac{\text{inside\_circle}}{\text{num\_samples}} \times 4\right)\)

# Estimate the value of Pi using simple Monte Carlo simulation
def estimate_pi(num_samples):
    inside_circle = 0
    for _ in range(num_samples):
        x, y = np.random.uniform(-1, 1, 2)
        if x**2 + y**2 <= 1:
            inside_circle += 1
    return (inside_circle / num_samples) * 4

num_samples = 10000
pi_estimate = estimate_pi(num_samples)
print(f"Estimated Pi: {pi_estimate}")

>>> 3.143
    

Sometimes these methods can be more abstract than estimating a single value. Below we have an example of using a Monte Carlo Simulation to simulate Brownian motion, or the random movement of particles suspended in a fluid (liquid or gas) resulting from collisions with the fast-moving molecules of the fluid.

def brownian_motion_gif(num_particles=100, num_steps=1000, delta_t=1, diffusion_coefficient=1,
 xlim=(-30, 30), ylim=(-30, 30), gif_name='brownian_motion.gif'):
    # Step 1: Define the domain of possible inputs (initial positions and random displacements)
    positions = np.zeros((num_particles, 2))
    all_positions = np.zeros((num_steps, num_particles, 2))

    # Simulate the Brownian motion
    # Step 2: Generate inputs randomly from a probability distribution (random displacements)
    for t in range(num_steps):
        # Random displacements
        displacements = np.sqrt(2 * diffusion_coefficient * delta_t) * np.random.normal(size=(num_particles, 2))
        # Step 3: Perform a deterministic computation (update positions)
        positions += displacements
        all_positions[t] = positions

    # Create GIF in memory
    # Step 4: Aggregate the results (store and visualize positions)
    

Monte Carlo methods offer a straightforward approach to solving numerical problems through random sampling, making them versatile and widely applicable. However, for problems involving intricate distributions, we need a more sophisticated technique. Markov Chain Monte Carlo (MCMC) methods build upon the foundation of Monte Carlo methods by incorporating Markov chains, allowing for a more nuanced and effective exploration of the target distribution.

MCMC Methods

Markov Chain Monte Carlo (MCMC) methods are a class of algorithms used to sample from complex probability distributions (denoted \(p(x)\)), particularly when direct sampling from this distribution is difficult or impossible. By constructing a Markov chain that has the desired distribution as its stationary distribution, MCMC methods generate a sequence of samples \((x_0, x_1, x_2, \ldots, x_n)\) that approximate the target distribution over time.

It is important to note that random samples from a probability distribution should be statistically independent. Here we only have the weaker assumption that our samples have the Markov Property, which leads to the samples used in MCMC methods being autocorrelated. Correlations of samples introduce a host of issues and a host of ways to counteract them.

Several MCMC algorithms have been developed to address various sampling challenges, with the Metropolis-Hastings algorithm and Gibbs sampling being among the most widely used. From here we will detail these two methods.

Metropolis-Hastings Algorithm

If you have a known, but hard to sample from distribution \(p(x)\), the Metropolis-Hastings algorithm provides a way to generate a Markov chain whose stationary distribution is \(p(x)\). This is not only useful for generating a sequence for sampling from a distribution, but also for performing integration over an otherwise intractable distribution.

Unlike simple random sampling methods, Metropolis-Hastings can handle target distributions that are not normalized and are defined on complex, high-dimensional spaces. It works by proposing moves to new states based on a proposal distribution and then accepting or rejecting these moves with a probability that ensures detailed balance, thereby maintaining the correct stationary distribution.

Target Distribution: Define the target distribution \(p(x)\) from which you want to sample. This is the distribution that we want our Markov Chain’s stationary distribution to be equal to.

Proposal Distribution: Choose a proposal distribution \(q(x’ \mid x)\) that suggests new states \(x’\) based on the current state \(x\). This corresponds to the Markov Chain’s transition matrix.

Sampling: Use the Metropolis-Hastings algorithm to generate a large number of samples \(\{x_1, x_2, \ldots, x_N\}\) from \(p(x)\).

Formally, the algorithm can be written as:

1. Initialise
   • Pick an initial state \(x_0\)
   • Set \(t = 0\)
2. Iterate
   • Generate a random candidate state \(x’\) according to \(q(x’ \mid x_t)\)
   • Calculate the acceptance probability \(A(x’, x_t) = \min\left( 1, \frac{p(x’)}{p(x_t)} \frac{q(x_t \mid x’)}{q(x’ \mid x_t)} \right)\)
3. Accept (\(x_{t+1} = x’\)) or reject (\(x_{t+1} = x_t\))
   • If \(A(x’ \mid x_t) \geq 1\), automatically accept the change.
   • If \(A(x’ \mid x_t) < 1\), accept with probability \(A(x' \mid x_t)\)

It’s important to note that in general, there is no exact answer for what distribution \(q(x’ \mid x)\) you should use.

Now let’s look at an example of sampling from the normal distribution. We can do so using the following code.

def target_distribution(x):
    # Example target distribution: a standard normal distribution
    return np.exp(-0.5 * x**2) / np.sqrt(2 * np.pi)

def proposal_distribution(x):
    # Example proposal distribution: a normal distribution centered at x with some standard deviation
    return np.random.normal(x, 1)

def metropolis_hastings(target_dist, proposal_dist, initial_state, num_samples):
    samples = []
    current_state = initial_state

    for _ in range(num_samples):
        proposed_state = proposal_dist(current_state)
        acceptance_ratio = target_dist(proposed_state) / target_dist(current_state)

        if np.random.rand() < acceptance_ratio:
            current_state = proposed_state

        samples.append(current_state)

    return np.array(samples)
    

And as we draw more samples we can see the normal distribution start to form. You should also notice how the auto correlation causes a very non-Normal distribution for the first few steps. To avoid this, a burn-in period is often used where you let the algorithm run for a sufficient number of steps before beginning to sample from it.

You may have noticed that despite being named "Monte Carlo Markov Chain", there is no reference to our Markov Chain class being used in the Metropolis Step. Why is that?

In MCMC methods, the concept of "state" refers to the value of the variables being sampled at a given point in time. As the algorithm progresses, it generates a sequence of samples, each of which represents a state of the Markov chain. This sequence of states is intended to explore the target probability distribution.

In practice, MCMC methods do not explicitly construct a Markov chain but rather implicitly create one through the sequence of accepted states (samples). Each sample is a state, and the transitions between these states are guided by the algorithm's rules. The key goal is to ensure that the long-run behavior of the chain (i.e., the distribution of the samples) matches the target distribution, allowing us to use these samples for statistical inference, optimization, or other applications.

Using Metropolis-Hastings for numerical integration

Integrating a function over a distribution is a concept commonly used in probability and statistics, especially in the context of expected values. Consider a space \(\Omega \subset \mathbb{R}\) and a distribution \(p(x)\) over \(\Omega\). We can now compute the integral:

\[ I = \int_{\Omega} f(x) p(x) \, dx \]

where \(f(x)\) is a measurable function of interest.

In many practical scenarios, the probability function \(p(x)\) may be such that analytical integration is infeasible. The Metropolis-Hastings algorithm can be used to approximate this integral by generating samples from the distribution \(p(x)\), and then estimating via:

\[ I \approx \frac{1}{N} \sum_{i=1}^{N} f(x_i) \]

where \(N\) is the number of samples and \(x_i\) are the samples drawn from \(p(x)\).We can go this, because when \(p(x)\) is a probability density function (pdf), the integral represents the expected value (or mean) of \(p(x)\) if it were transformed by the function \(f(x)\).

For this example we are going to be integrating

\[ I = \int_{\mathbb{R}} \left((x_1^2) + (x_2^2)\right) p(x_1, x_2) \, dx_1 \, dx_2 \]

where \(p(x)\) is the multivariate normal function with a mean vector of \([0,0]\) and a covariance matrix of

\[ \begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \end{bmatrix} \]

For this example we have chosen a function that we are able to integrate in order to verify that our method works. If you do it by hand, you'll find that this integral equals \(2\). If we run the following code, we can see our sampling, and what our final estimate for this integral is.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal


def target_distribution(x, y):
    # Bivariate normal distribution
    mu = np.array([0, 0])
    sigma = np.array([[1, 0.5], [0.5, 1]])
    return multivariate_normal.pdf([x, y], mean=mu, cov=sigma)

def proposal_distribution(x, y):
    # Proposal distribution: normal distribution centered at (x, y)
    # Our proposal density is symmetric, so g(x|x') = g(x'|x), makes the acceptance ratio easier to compute
    step_size = 0.5
    return np.random.normal([x, y], step_size, 2)

def metropolis_hastings_2d(target_dist, proposal_dist, initial_state, num_samples):
    samples = []
    current_state = initial_state

    for _ in range(num_samples):
        proposed_state = proposal_dist(*current_state)
        acceptance_ratio = target_dist(*proposed_state) / target_dist(*current_state)

        if np.random.rand() < acceptance_ratio:
            current_state = proposed_state

        samples.append(current_state)

    return np.array(samples)

# Parameters
initial_state = [0, 0]
num_samples = 10000

# Generate samples using Metropolis-Hastings algorithm
samples = metropolis_hastings_2d(target_distribution, proposal_distribution, initial_state, num_samples)

# Function to integrate
f = lambda x, y: x**2 + y**2

# Running average of the integral estimate
f_values = np.array([f(x, y) for x, y in samples])
running_avg = np.cumsum(f_values) / np.arange(1, num_samples + 1)
    

Similar to before there is a bit of a burn-in period before we are able to get a good approximation. Unfortunately there is no way to determine exactly how long the burn in period should be (that I am aware of). There are certain methods like an auto-correlation analysis, or the use of the Gelman-Rubin statistic that let you make statements about the convergence to the stationary distribution. However, it often comes down to visual inspection, or even letting your method run multiple times with different burn in periods, and just choosing the best.

Beyond this particular algorithm, MCMC methods form an extraordinarily deep field of research in areas like Adaptive MCMCs, parallel/distributed MCMCs, and Hamiltonian Monte Carlo Methods. Hopefully this post at least gives you an idea of their intention and potential power. For another MCMC, I've made a post on Gibbs Sampling that you can also check out.

---