Gibbs sampling is one of the fundamental modern Markov Chain Monte Carlo (MCMC) methods. Named after the American physicist Josiah Willard Gibbs, but developed by the brothers Stuart and Donald Geman, this technique was initially developed to address problems in image processing but quickly found applications across various fields of statistics and machine learning. At its core, Gibbs sampling is an algorithm for drawing samples from a multivariate probability distribution when direct sampling is difficult, but the conditional distribution of each variable is known and easy to sample.
The importance of Gibbs sampling lies in its ability to break down complex, high-dimensional problems into a series of simpler, lower-dimensional ones. This makes it particularly useful in Bayesian inference, where we often need to estimate posterior distributions that are analytically intractable. By iteratively sampling each variable conditioned on the current values of the others, Gibbs sampling provides a practical way to explore and characterize complex probability distributions.
This post is more or less a part 2 to my post about “Markov Chains and the Metropolis-Hastings Algorithm”, which is fitting as Gibbs Sampling is actually a special case of that algorithm. If you’re reading it and you get lost, check out that post as any needed background should be in there.
The post goes as following
- Intro to Gibbs Sampling
- Example #1
- How to Choose a Sampler
- Example #2
If you see any issues, please send me an email. If you want to see any of the code that went into this, check out the notebook at https://github.com/HarrisonSantiago/WebsiteNotebooks
Understanding Gibbs Sampling
Gibbs sampling is a powerful method for generating samples from complex, difficult to sample from, multivariate probability distributions, where direct sampling from joint distributions is prohibitively difficult. Rather than tackle that beast, it leverages the conditional distributions, which are typically more manageable than their joint counterparts. The algorithm proceeds by iteratively sampling each variable from its conditional distribution, contingent upon the current values of all other variables in the system. This step-by-step approach gradually converges to the desired joint distribution of all variables, effectively building a comprehensive picture of the probabilistic landscape.
The mechanics of Gibbs sampling can be conceptualized as a sequential update process. In each iteration, the algorithm generates a new instance for each variable, drawing from its conditional distribution given the most recent values of the other variables. This sequence of samples forms a Markov chain, whose stationary distribution converges to the target joint distribution. To make this more clear, each state in this Markov chain represents a complete set of values for all variables in the system under study. For instance, in a model with three variables /\(X\), \(Y\), and \(Z\), a single state would be characterized by a specific combination of the sampled values,s \((x_i, y_j, z_k)\). As with all MCMC methods, the transition matrix is implicitly, rather than explicitly, constructed.
To be specific, the sampling process is as such:
- Sequential Updating: Starting from an initial state (initial values for all variables), one variable is selected and its value is updated by sampling from its conditional distribution given the current values of all other variables. For example, you might first update \(X\) by sampling from \(p(X \mid Y=y_j, Z=z_k)\).
- Cyclic or Random Order: After updating \(X\), you might then update \(Y\) by sampling from \(p(Y \mid X=x_{\text{new}}, Z=z_k)\), and then \(Z\) from \(p(Z \mid X=x_{\text{new}}, Y=y_{\text{new}})\). This sequence can proceed in a cyclic order or randomly.
- New State Formation: Each round of updates (after all variables have been sampled once) generates a new state in the Markov Chain. This new state is dependent only on the state immediately preceding it (the values of variables from the last iteration), fulfilling the Markov property that the future state depends only on the current state and not on the sequence of events that preceded it.
Example #1
I thought it would be best to use two examples to show how Gibbs Sampling is implemented. The first one is intended to show how we use those steps to create the transition mechanism. However, the work for creating our samplers \(p(x|y)\) and \(p(y|x)\) is very hand-wavy, and will be explained later. For now, just accept that they are true. Imagine that you’re sampling from a joint distribution with the following form:
\[ f(x,y) = \frac{1}{C} \exp\left(-\frac{x^2 y^2 + x^2 + y^2 – 8x – 8y}{2}\right) \]
Since we don’t know what the normalizing constant \( C \) is, we can’t sample from this distribution using conventional methods. However, since the conditional distribution of one variable given all others is proportional to the joint distribution, Gibbs sampling allows us to do so.
After some simplification (completing the square and throwing all factors that do not involve \( x \) into \( g(y) \), and vice versa), we find the following conditional distributions:
\[ p(x \mid y) = g(y) \exp\left(-\left(x – \frac{4}{1 + y^2}\right)^{\frac{2(1 + y^2)}{2}}\right) \]
and
\[ p(y \mid x) = g(x) \exp\left(-\left(y – \frac{4}{1 + x^2}\right)^{\frac{2(1 + x^2)}{2}}\right) \]
Since these are Normal distributions, we can rewrite these as
\[ x \mid y \sim \mathcal{N} \left( \frac{4}{1 + y^2} , \sqrt{\frac{1}{1+y^2}}\right) \]
and
\[ y \mid x \sim \mathcal{N} \left( \frac{4}{1 + x^2} , \sqrt{\frac{1}{1+x^2}}\right) \]
From here we can build a sampler, and test our method. Like with any MCMC, we want to include some burn-in period.
#Define the conditional distribution functions
def sig(z):
return np.sqrt(1.0 / (1.0 + z * z))
def mu(z):
return 4.0 / (1.0 + z * z)
def sample_x_given_y(y):
sigma_x = sig(y)
mu_x = mu(y)
return np.random.normal(mu_x, sigma_x)
def sample_y_given_x(x):
sigma_y = sig(x)
mu_y = mu(x)
return np.random.normal(mu_y, sigma_y)
# Gibbs sampling parameters
num_samples = 10000
burn_in = 2000 # Burn-in period
# Step 1 (give initial values)
samples = np.zeros((num_samples, 2))
x = 1.0
y = 6.0
# Gibbs sampling
for i in range(num_samples):
# 2) Cyclic Ordering
x = sample_x_given_y(y)
y = sample_y_given_x(x)
# 3) New state formation
samples[i, 0] = x
samples[i, 1] = y
# Discard burn-in samples
samples = samples[burn_in:]
To see how well we did, below I have plotted the joint distribution for an arbitrary C. Then the blot to the right of it is our sampled points. Below that, and plot our marginals. We can see that these match what we would expect to see if we projected our contour plot onto each of the axes.
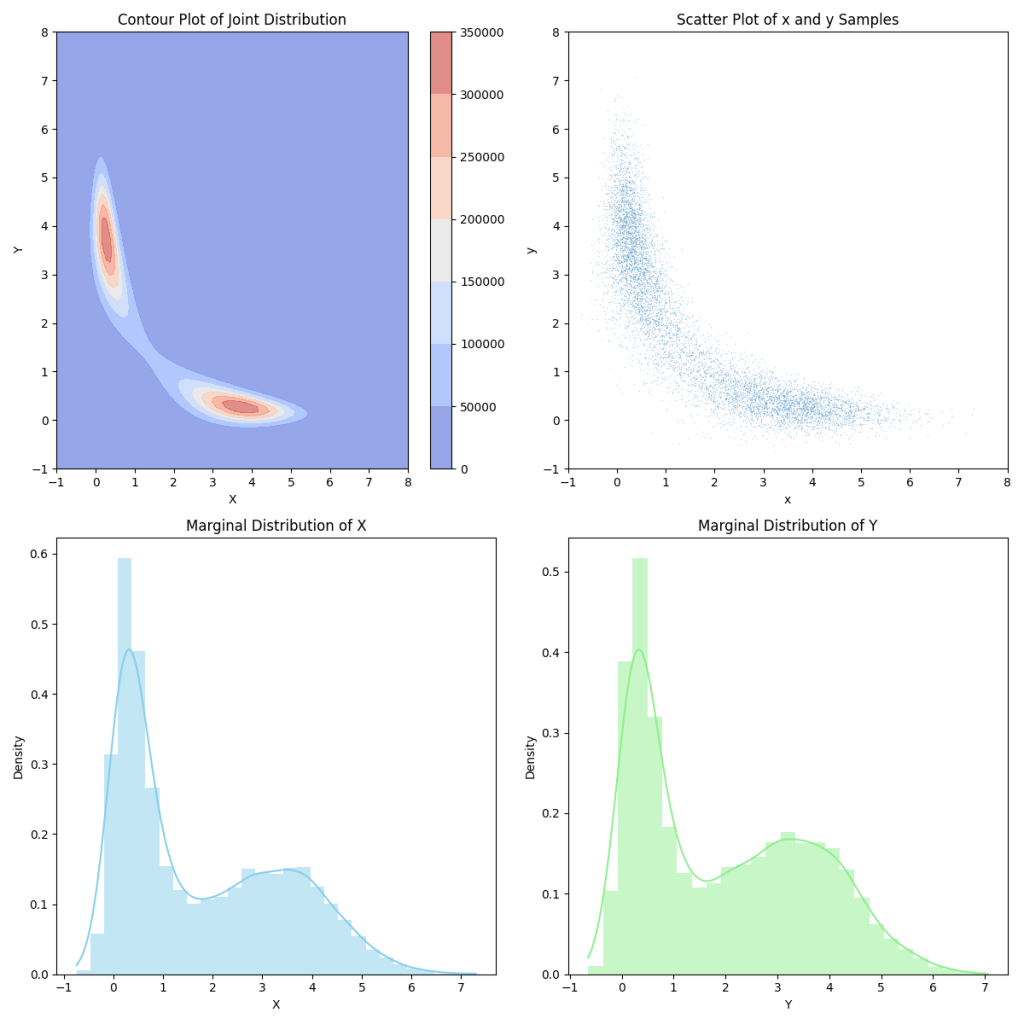
And what about the joint distributions? Well if we take a look at those, we can see that they are the normal distributions that we expect. In each of these gifs, we are taking the conditional for different points of \(X\) and \(Y\). All in all, this seems to have worked.


Choosing Your Sampler
Hopefully that toy example was enough to convince you that Gibbs sampling works. However, now it’s time for us to learn how we construct our samplers. Frustratingly, there isn’t a very general method for how we do it. From what I’ve learned, it seems to be more of an art than anything else. When doing this MCMC method, a lot of the difficulty with this method comes from creating a sampler that is well-behaved. Loosely speaking, the best instructions are more of a guideline:
- Write down the posterior (joint) density function, most always in log-form. This is found as a product of the prior and the likelihood function.
- Eliminate all the factors that don’t depend on the current sampling variable (in effect marginalizing over them).
- Try to view the remaining factors as the log-density of a tractable distribution. This becomes your conditional sampling density.
- Write a program that samples from each of these tractable distributions.
You may have also noticed that suddenly I switched to talking about posteriors, priors, and likelihood functions. That is because Gibbs sampling is very strongly associated with Bayesian analysis, and in practice it’s uncommon to see it in other contexts. To be brief on why, Bayesian analysis often involves complex, high-dimensional posterior distributions, which we’ve learned is what Gibb’s sampling is suited for. Moreover, these distributions often have a natural conditional independence structure, and Gibbs sampling can exploit this structure. Beyond that, in many Bayesian models, conjugate priors are used (more information on this later). These priors result in conditional distributions that have known, easily sampled forms.
Example #2
Building off that, our second example will some Bayesian linear regression. Here is a quick refresher on some definitions, feel free to skip until the horizontal line.
The likelihood function, \(L(\theta \mid x)\), is defined as the joint probability mass of observed data, viewed as a function of model parameters. What this means, if that gives the likelihood of a distribution’s parameter vector \(\theta\), under a set of observed data \(x\). Numerically, this is the same as the probability function \(p(x \mid \theta)\), which gives the probability of the observed data, \(x\), assuming \(\theta\) is true. If we let \(X\) be a discrete random variable with probability mass function \(P\), which depends on \(\theta\), we can say \(L(\theta \mid x) = p_\theta(x) = P_\theta(X=x)\).
Bayes’ Theorem describes the probability of an event, based on prior knowledge of conditions that may be related. Formally, it is expressed as \(p(\theta \mid x) = \frac{p(x \mid \theta)}{p(x)} p(\theta)\) where \(p(\theta \mid x)\) is called the posterior, \(p(x \mid \theta)\) is the likelihood, \(p(\theta)\) is the prior, and \(p(x)\) is a normalizing constant.
If given a likelihood function, the posterior and prior are in the same probability distribution family, they are said to be conjugate distributions with respect to that likelihood. The primary advantage of conjugate priors is that they result in posterior distributions of the same family as the prior distribution. This mathematical convenience often allows for closed-form solutions to the posterior, eliminating the need for complex numerical integration or approximation methods.
Finally, Bayesian linear regression extends traditional linear regression by treating model parameters as random variables with prior distributions, rather than fixed but unknown constants. It combines these priors with observed data to compute posterior distributions of the parameters, providing not just point estimates but full probability distributions that quantify uncertainty in the model coefficients and predictions.
Let’s assume we have a set data points \((x_i, y_i), i = 1, \ldots, N\). We can construct our regression model as:
\[ y_i \sim \mathcal{N}(\beta_0 + \beta_1 x_i, \frac{1}{\tau}) \] where we define \(\tau\) to be the reciprocal of the variance, equivalently this is: \[ y_i = \beta_0 + \beta_1 x_i + \epsilon, \epsilon \sim \mathcal{N}(0, \frac{1}{\tau}) \]
By making the ever-so-made assumption of i.i.d. observations, we can easily write our likelihood (prior) as:
\[ p(x,y \mid \beta_0, \beta_1, \tau) = \prod_{i=1}^{N} \mathcal{N}(\beta_0 + \beta_1 x_i, \frac{1}{\tau}) \]
For convenience, we will now place conjugate priors on \(\beta_0\), \(\beta_1\), and \(\tau\). That means for those three parameters, we can say
\[ \beta_0 \sim \mathcal{N}(\mu_0, \frac{1}{\tau_0}) \]
\[ \beta_1 \sim \mathcal{N}(\mu_1, \frac{1}{\tau_1}) \]
\[ \tau \sim \text{Gamma}(\alpha, \beta) \]
As a further explanation for some of these choices, if you look here and here, you can learn that using the inverse of the variance (or the precision), instead of variance has some advantages. One such advantage is if both the prior and the likelihood have Gaussian form, and the precision matrix of both of these exists (because their covariance matrix is full rank and thus invertible), then the precision matrix of the posterior will simply be the sum of the precision matrices of the prior and the likelihood.Similarly, the Gamma prior on \(\tau\) is useful as the gamma distribution is the conjugate prior for the precision of the normal distribution with known mean.
Now, lets start to construct our samplers using our guidelines from above.
For \(\beta_0\)
Here we want to find \(p(\beta_0 \mid \beta_1, \tau, x, y)\). We know from Bayes’ Theorem
\[ p(\beta_0 \mid \beta_1, \tau, x, y) \propto p(x,y \mid \beta_0, \beta_1, \tau) p(\beta_0) \]
From above, we know that
\[ p(x,y \mid \beta_0, \beta_1, \tau) = \prod_{i=1}^{N} \mathcal{N}(\beta_0 + \beta_1 x_i, \frac{1}{\tau}) \]
and
\[ \beta_0 \sim \mathcal{N}(\mu_0, \frac{1}{\tau_0}) \]
so we can say
\[ p(\beta_0 \mid \beta_1, \tau, x, y) \propto p(\beta_0) p(x,y \mid \beta_0, \beta_1, \tau) \]
or
\[ p(\beta_0 \mid \beta_1, \tau, x, y) \propto \exp\left(- \frac{(\beta_0 – \mu_0)^2}{2 \frac{1}{\tau_0}}\right) \prod_{i=1}^N \exp\left(- \frac{(y_i – \beta_0 – \beta_1 x_i)^2}{2 \frac{1}{\tau}} \right) \]
By going into log form (step 3) and pulling out constants, we get
\[ \log(p(\beta_0 \mid \beta_1, \tau, x, y)) \propto – \frac{\tau_0}{2}(\beta_0 – \mu_0)^2 – \frac{\tau}{2} \sum_{i=1}^N (y_i – \beta_0 – \beta_1 x_i)^2 \]
A bit of algebra, and dropping all the terms that don’t involve \(\beta_0\) (step 2) gives us
\[ \beta_0 \left( \tau_0 \mu_0 + \tau \sum_i (y_i – \beta_1 x_i)\right) – \beta_0^2 \left(\frac{\tau_0}{2} + \frac{\tau}{2}\right) \]
Looking at the normal function through an alternative parameterization of the normal function where it has parameters \(\theta_1 = \frac{\mu}{\sigma^2}\) and \(\theta_2 = \frac{-1}{2\sigma^2}\) with natural statistics \(x\) and \(x^2\), we can see that our previous log-posterior implies that the conditional sampling distribution is
\[ p(\beta_0 \mid \beta_1, \tau, x, y) \sim \mathcal{N} \left( \frac{\tau_0 \mu_0 + \tau \sum_i (y_i – \beta_1 x_i)}{\tau_0 + \tau N}, \frac{1}{\tau_0 + \tau N} \right) \]
Now, let’s finally turn that into a python function (step 4).
def sample_beta_0(y, x, beta_1, tau, mu_0, tau_0):
N = len(y)
precision = tau_0 + tau * N
mean = tau_0 * mu_0 + tau * np.sum(y - beta_1 * x)
mean /= precision
return np.random.normal(mean, 1 / np.sqrt(precision))
Now let’s do the same for \(\beta_1\). These are more or less the same steps, so here we’ll be much quicker about it.
\[ p(\beta_1 \mid \beta_0, \tau, x, y) \propto – \frac{\tau_1}{2}(\beta_1 – \mu_1)^2 – \frac{\tau}{2}\sum_{i=1}^N (y_i – \beta_0 – \beta_1 x_i)^2 \]
After the algebra, we get
\[ p(\beta_1 \mid \beta_0, \tau, x, y) \propto \beta_1 \left( \tau_1 \mu_1 + \tau \sum_i (y_i – \beta_0)x_i \right) + \beta_1^2 \left( – \frac{\tau_1}{2} – \frac{\tau}{2} \sum_i x_i^2 \right) \]
And from there we can see
\[ \beta_1 \mid \beta_0, \tau, \mu_1, \tau_1, x, y \sim \mathcal{N} \left( \frac{\tau_1 \mu_1 + \tau \sum_i (y_i – \beta_0) x_i}{\tau_1 + \tau \sum_i x_i^2}, \frac{1}{\tau_1 + \tau \sum_i x_i^2} \right) \]
We turn this into a python function by saying:
def sample_beta_1(y, x, beta_0, tau, mu_1, tau_1):
N = len(y)
precision = tau_1 + tau * np.sum(x * x)
mean = tau_1 * mu_1 + tau * np.sum( (y - beta_0) * x)
mean /= precision
return np.random.normal(mean, 1 / np.sqrt(precision))
And now we get to the update for \(\tau\), our first non-Gaussian distribution. Earlier we defined it as a Gamma distribution (\(\text{Gamma}(\alpha, \beta)\)), which has a density
\[ p(x) \propto x^{\alpha – 1} e^{-\beta x} \]
and so the log dependency is given by
\[ \log(p(x)) \propto (\alpha – 1) \log(x) – \beta x \]
That being said, we want
\[ p(\tau \mid \beta_0, \beta_1, y, x) \propto p(y, x \mid \beta_0, \beta_1, \tau) p(\tau) \]
We’ve already found the first term \(\prod_{i=1}^N \mathcal{N}\left( y_i \mid \beta_0 + \beta_1 x_i, \frac{1}{\tau} \right) \) numerous times, and defined the second term as \(\text{Gamma}(\tau \mid \alpha, \beta)\). If we look at the log density of this, we get the moderately familiar
\[ \frac{N}{2} \log(\tau) – \frac{\tau}{2} \sum_i (y_i – \beta_0 – \beta_1 x_i)^2 + (\alpha – 1) \log(\tau) – \beta \tau \]
which if we rearrange as
\[ \left( \frac{N}{2} + \alpha – 1 \right) \log(\tau) – \left( \frac{\sum_i (y_i – \beta_0 – \beta_1 x_i)^2}{2} + \beta \right) \tau \]
which looks a lot like our log density for the Gamma distribution above. This implies that the conditional sampling density we are looking for is
\[ \tau \mid \beta_0, \beta_1, \alpha, \beta, x, y \sim \text{Gamma}\left( \alpha + \frac{N}{2}, \beta + \sum_i \frac{(y_i – \beta_0 – \beta_1 x_i)^2}{2} \right) \]
Let’s finally turn this into Python.
# Numpy uses the kappa/theta parameterization of
# the gamma distribution rather than alpha/beta,
def sample_tau(y, x, beta_0, beta_1, alpha, beta):
N = len(y)
alpha_new = alpha + N / 2
resid = y - beta_0 - beta_1 * x
beta_new = beta + np.sum(resid * resid) / 2
return np.random.gamma(alpha_new, 1 / beta_new)
Now to test it out, lets create some true values for these parameters and then a set of data from from.
beta_0_true = -1
beta_1_true = 2
tau_true = 1
N = 100
x = np.random.uniform(low = 0, high = 4, size = N)
y = np.random.normal(beta_0_true + beta_1_true * x, 1 / np.sqrt(tau_true))

Now that we’ve constructed our dataset, let’s try to recover the original true parameters. First we initialize our guesses, some hyperparameters for the samplers, and let out algorithm run.
## specify initial values
init = {"beta_0": 0,
"beta_1": 0,
"tau": 2}
## specify hyper parameters
hypers = {"mu_0": -1,
"tau_0": 1,
"mu_1": 1,
"tau_1": 1,
"alpha": 2,
"beta": 1}
def gibbs(y, x, iters, init, hypers):
assert len(y) == len(x)
beta_0 = init["beta_0"]
beta_1 = init["beta_1"]
tau = init["tau"]
trace = np.zeros((iters, 3)) ## trace to store values of beta_0, beta_1, tau
for it in range(iters):
beta_0 = sample_beta_0(y, x, beta_1, tau, hypers["mu_0"], hypers["tau_0"])
beta_1 = sample_beta_1(y, x, beta_0, tau, hypers["mu_1"], hypers["tau_1"])
tau = sample_tau(y, x, beta_0, beta_1, hypers["alpha"], hypers["beta"])
trace[it,:] = np.array((beta_0, beta_1, tau))
trace = pd.DataFrame(trace)
trace.columns = ['beta_0', 'beta_1', 'tau']
return trace
iters = 1000
trace = gibbs(y, x, iters, init, hypers)
Below we have two visualizations our the trace data. The first is the value of the guess for each parameter over time, and we can see how our algorithm converged to near the true parameters pretty quickly. The second is a histogram of all those values over time. Here we can see the effect of choosing a normal distribution for our conditionals, and how we were rarely far away from the true values.


Hopefully this post has provided some intuition for Gibbs sampling, offering a foundation for implementing this method in your own projects. While we’ve covered the core concepts, it’s worth noting that there are several variations of Gibbs sampling designed to overcome various computational and statistical limitations. As you delve deeper into this topic, you’ll discover that Gibbs sampling is not just a powerful tool on its own, but also a gateway to understanding more advanced MCMC techniques that form the backbone of modern computational statistics.